8x8 lik satranç tahtasına en az kaç at yerleştirilmeli ki tüm kareler korunsun?
Bakış Açısı
Eğer aklınıza hemen küme kapsama problemi geldiyse ve çözümü merak ediyorsunuz bu kısmı atlayıp sayfayı aşağı kaydırabilirsiniz ama varsayalım ki aklınıza küme kapsama problemi gelmedi. İlk başta benim aklıma gelmemişti ama yine de düşünelim nasıl çözeceğiz?
$$i, j \in {1,2,3,4,5,6,7,8}$$
Öncelikle probleme ait uzayı tanımlamak lazım. 2 boyutlu uzayda herbir i ve j için herbir kareyi K(i, j) tanımlasak yeterli olacaktır.
At, bir eksende 2 kare, diğer eksende 1 kare giderek ‘L’ şeklinde hareket eder. (2,1) (1,2) (-2,1)…
Buna göre $K(i,j)$ karesindeki atın koruyacağı (gidebileceği) kareler:
K(i + 2, j - 1), | K(i + 1, j + 2) K(i + 2, j + 1), | K(i + 1, j - 2) K(i - 2, j + 1), | K(i - 1, j + 2) K(i - 2, j - 1), | K(i - 1, j - 2)
olacaktır. Örnek bir kare için K(4,5) görselleştirelim:
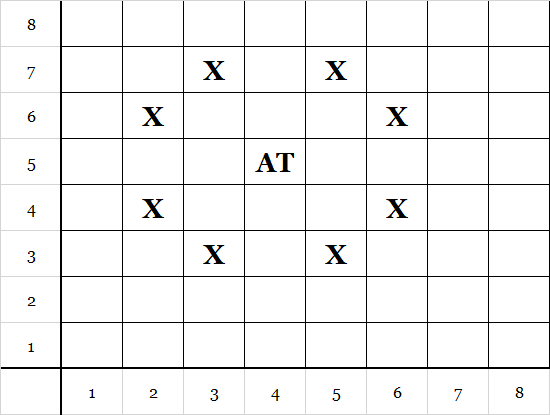
K(i, j)‘yi eğer at atandıysa 1,
aksi halde 0 alacak binary değişken olarak tanımlayalım. Amaç fonksiyonu toplam at sayısını minimize etmek üzere tanımlayalım.
$$\min Z = \sum_i\sum_j K(i,j)$$
Geldik zor kısmına, öyle kısıtlar yazmalıyız ki tüm karelerin korunmasını sağlasın. Vaktinde (bir iki yıl önce) birkaç saat uğraşmıştım bu bakış açısı ile kısıtları oluşturmaya. Epey de ilerledikten sonra boşa kürek çektiğimi farketmiştim. Tekrar burada o modeli anlatmayacağım ama ikinci bir binary değişken (karenin korunup korunmadığına dair) daha tanımlayıp işleri karmaşıklaştırmıştım.
Şimdi doğru bakış açısıyla probleme tekrar bakalım.
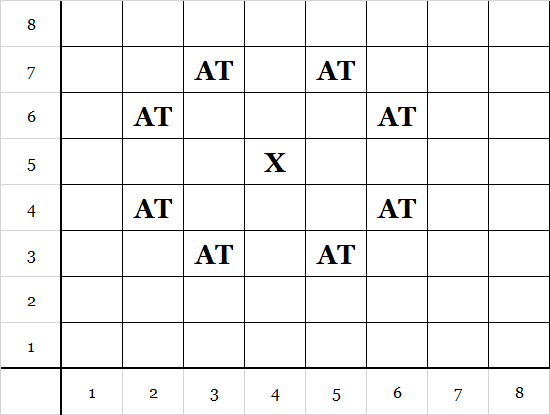
Sözlü ifade etmek gerekirse; bir ‘X’ noktasını korumak için, yukarıdaki 8 alternatif konuma ‘AT’ yerleştirebilir. Diğer bir deyişle, Bir atın koruduğu karelere değil, bir kareyi koruyan atlara bakıyoruz. Buradan sonrası küme kapsama problemi ve çözümü belli.
Burada biraz felsefe yapacağım, hayattaki problemler karşısında önce problemi iyi anlamak, tanımlamak gerektiği ile ilgili. Bir konuya farklı bakış açılarıyla yaklaşabilmeliyiz; çünkü çözüme her zaman birden fazla yoldan ulaşabilir. Genellikle o yollardan bir ya da birkaç tanesi diğerlerine göre daha zahmetsiz olur.
Matematiksel Model
$$\min \sum_i\sum_j X_{i,j}$$
subject to;
$$ X_{i+2,\ j+1} + X_{i+2,\ j-1} + X_{i-2,\ j+1} + X_{i-2,\ j-1} + X_{i+1,\ j+2}+ X_{i+1,\ j-2} + X_{i-1,\ j+2}+X_{i-1,\ j-2} + X_{i,\ j}\ge 1 \qquad \forall {i,j} $$
$$X_{i,j} \in {0,1} \qquad \forall {i,j}$$
Bir at, yukarıdaki resimlerden de anlaşıldığı üzere çevresindeki 8 noktayı koruyabiliyor. Ek olarak kendi bulunduğu hücreyi de koruyor. X(i,j) hücresini atladığımızda modelimiz eksik ve sonucumuz da yanlış olur.
GAMS
GAMS syntaxında aşağıdaki gibi yazılabilir:
SETS
I /1*8/;
ALIAS (I,J);
VARIABLE Z;
BINARY VARIABLE X(I,J);
EQUATION OBJECTIVE, CONSTRAINT;
OBJECTIVE.. Z =E= SUM(i, SUM(j, X(i,j)));
CONSTRAINT(i,j).. X(i+2,j-1) + X(i+2, j+1) +
X(i-2,j+1) + X(i-2, j-1) +
X(i+1, j+2) + X(i+1, j-2) +
X(i-1, j+2) + X(i-1,j-2)+ X(i,j) =G= 1;
MODEL set_covering /all/;
SOLVE set_covering USING MIP MINIMIZE Z;
option optcr = 0.0;
DISPLAY X.L;
Optimal Çözüm
Model, CPLEX ile çözdürüldüğünde optimal çözümde amaç fonksiyonu değeri 12 olarak bulunmuştur, çözüm aşağıdadır.
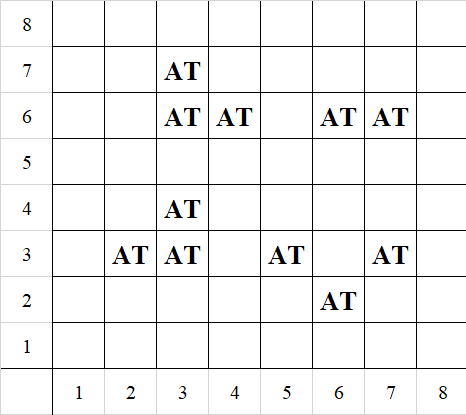
Ek olarak, burada herbir (i,j) için gelen kısıtlarda, eşitsizliğin sol tarafı herbir karenin kaç at tarafından korunduğu bilgisini verir. Ne kadar ‘güçlü’ korunduğu şeklinde de açıklanabilir.
GAMS kodunda bir Positive Variable P(I,J) tanımlayıp sol tarafı P(i, j)‘ye eşitleyerek aşağıdaki matrise ulaşabiliriz:
1 2 3 4 5 6 7 8
1 1 1 1 3 1 1 1 1
2 1 1 1 3 1 1 1 1
3 1 1 1 1 3 1 1 1
4 1 1 3 4 4 1 3 3
5 3 3 1 4 4 3 1 1
6 1 1 1 3 1 1 1 1
7 1 1 1 1 3 1 1 1
8 1 1 1 1 3 1 1 1
Beklendiği gibi her kare en az 1 at tarafından korunuyor. Merkeze yakın kareler daha güçlü korunuyor. P(1,4), P(2,4), P(5,1), P(5,2), P(5,3) gibi…
