Slope of a line
$$ y=mx+b $$
m is the slope of the line. How to find the slope of a line or the equation of a line where you have 2 points?
$$ \frac{\Delta y}{\Delta x}=\frac{y_1-y_2}{x_1-x_2} $$
Slope of a tangent line
$f'(x)$ returns the slope of a tangent line to $f(x)$ at $x$.
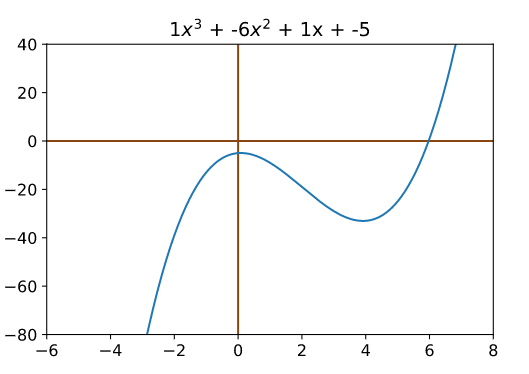
$$f(x) = x^3-6x^2+x-5$$, Find the equation of the tangent line to graph $f(x)$ at $x=1$.
Let’s say $g(x) = mx +b$ is the tangent line.
$$f'(x) = 3x^2-12+1$$
$$f'(1) = -8$$
$$f(1) = - 9$$
This means the slope of $g(x)$ is $-8$ and $g(1) = -9$.
As a result, $g(x) = -8x -1$
Diğer bir deyişle, $f'(x)$, $f(x)$‘in x noktasındaki tanjant doğrusunun eğimine karşılık gelir. Buna bağlı olarak kritik noktalarda $f’(x) = 0$ veya tanımsızdır. Min/Max noktalarında $f'(x) = 0$‘dır ve tanjant doğrusu düz olup eğimi sıfırdır.
Critical and Extremum Points
Alttaki resmi inceleyelim. Yukarıda da bahsettiğim gibi, birinci türev sıfır ve tanımsız olacaktır kritik noktarda ve bu kritik noktalar fonksiyonun içinde kalan (non-endpoints) noktalardır.
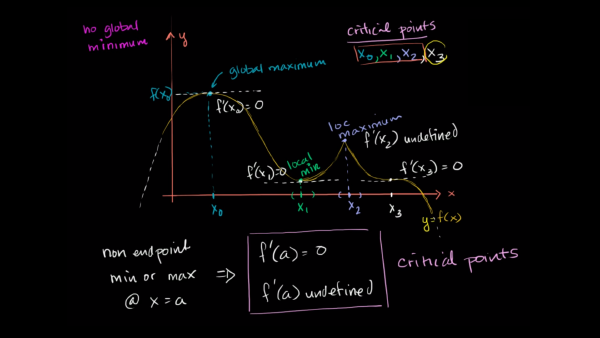
0, 1, 2 ve 3. noktalar kritik noktalardır. 2. noktada türev tanımlı değildir. Çünkü böyle bir uçta, tanjant doğrusun sonsuz şekilde çizebiliriz. Diğer noktalarda ise türev sıfırdır ya da o noktada çizilecek tanjant doğrusunun eğimi sıfırdır.
Şekle bakıldığında tüm kritik noktalarda max ya da min noktası (extremum) oluşmadığı görülür. $f’(x_3) = 0$ olmasına rağmen extremum noktası değildir.
Öyleyse bir noktanın extremum noktası olduğunu nasıl tespit ederiz?
Eğer, bir noktada tanjant doğrusu negatiften pozitife ya da pozitiften negatife geçiyorsa o nokta extremum noktasıdır.
$f'(x)>0 \to f'(x)<0$ : Maximum Point
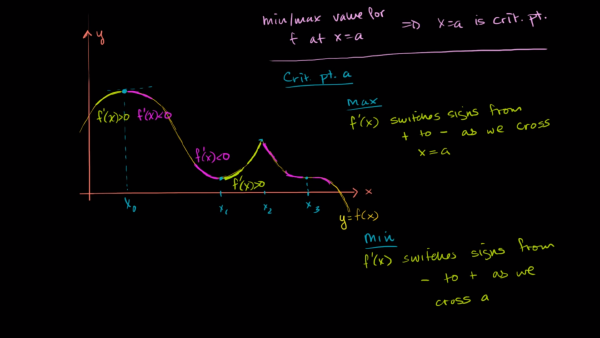
Dikkat edersek, $x_3$ noktasından önce fonksiyon azalıyor ve türev sıfırdan küçük, aynı şekilde $x_3$ noktasından sonra da fonksiyon azalmaya devam ediyor.
Relation between $f(x),\ f'(x) \ and \ f''(x)$
Birinci türev bir noktada çizilecek tanjant doğrusunun eğimini verirken, ikinci türev de, türevin türevi olarak, fonksiyonun eğimindeki değişimi gösterecektir.
Resimdeki fonksiyonu, sırasıyla mor kısmı ve yeşil kısmı extremum noktalarından iki parça halinde ele alarak 4 parçada inceleyelim:
| 1. Kısım | 2. Kısım | 3. Kısım | 4. Kısım |
|---|---|---|---|
| maximum noktasına kadar | yeşil kısma kadar | minumum noktasına kadar | minumum noktasından sonrası |
| $f'(x)>0$ | $f'(x)<0$ | $f'(x)<0$ | $f'(x)<0$ |
| fonksiyon artmaktadır | fonksiyon azalmaktadır | fonksiyon azalmaktadır | fonksiyon artmaktadır |
| $f''(x)<0$ | $f''(x)<0$ | $f''(x)>0$ | $f''(x)>0$ |
| fonksiyon azalarak artmaktadır | fonksiyon azalarak azalmaktadır | fonksiyon artarak azalmaktadır | fonksiyon artarak artmaktadır |
| fonksiyonun eğimi azalmaktadır | fonksiyonun eğimi azalmaktadır | fonksiyonun eğimi artmaktadır | fonksiyonun eğimi artmaktadır |
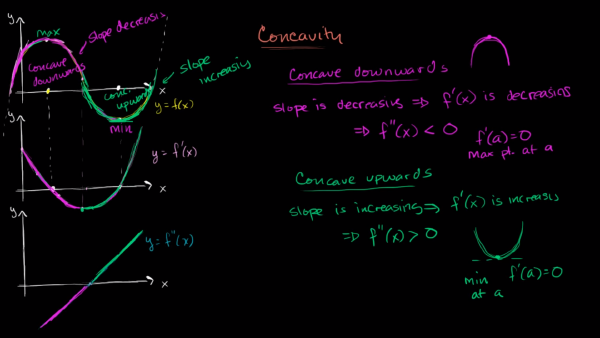
$f'(x)$‘in işaret değiştirdiği noktaya extremum point demiştik. $f’'(x)$‘in işaret değiştirdiği nokta ise inflection point denir.
Multivariable Functions
Eğer fonksiyon, multivariable ise $f(x,y,z,…)$ gibi… gradient fonksiyonu oluşturulup herbir değişken için kısmı türevine bakılır ve oluşan vektörün sıfır olduğu noktalar kritik noktalardır ve maximum ya da minumum noktaları olabilirler. Ancak multivariable fonksiyonlarla devreye giren yeni bir olasılık da saddle point‘tir. Saddle Point
Convex ve Concave’lik açısından değerlendiriğinde eğer fonksiyon, multivariable ise $f(x,y,z,…)$ gibi… Herbir değişken için ikinci kısmi türevine (second order partial derivative) bakılır ve Hessian matrisi oluşturulur.
