Linear Regression
Bu yazının amacı linear regresyona detaylı bir giriş yapmaktır. Regresyon analizinin amacı, değişken setleri arasındaki ilişkiyi tanımlamaktır. Bir bağımlı değişkeni, bir ya da birden fazla bağımsız değişkene bağlı olarak tahmin etmek için kullanılan modellerdir.
Linear Regresyon Nedir?
Linear Regresyon Nedir? Bunun Non-Linear’i de mi var?
Evet var, logistic’i, poisson’u, exponential’ı var. Bunlara ileride değineceğim. Bu yazıda yalnızca linear regresyon üzerinde duracağız.
Lineer regresyon lineer model gerektirir. Başlamadan önce, “lineer” nedir onu tanımlamak gerekir. Çünkü, genellikle “bir doğru” üzerinden anlatıldığı için, linear regresyon ile doğru çiziyormuşuz gibi bir algı oluşuyor. Amma velakin, doğrusal regresyon ile eğri(curve) de üretebiliriz. Nonlinear regresyon eğri ürettiği için nonlinear diye adlandırılmadığı gibi linear regresyonda doğru ürettiği için linear diye adlandırılmamıştır. Şaşırdınız mı? Dürüst olmak gerekirse, ben epey bi’ aydınlanma yaşamıştım.
Linear model nedir tanımlayalım:
Bir modelin linear olabilmesi için herbir terim; ya sabit ya da bir parametre ile tahminleyici değişkenin çarpımı olmalıdır. Linear eşitlik, tüm terimlerin toplam durumda olması ile elde edilir.
$$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \epsilon$$
İstatistikte, regresyon fonksiyonunun linear olması için, parametrelerin linear olması yeterlidir. Parametreler linear olduğu sürece, tahminleyici değişkenler ile oynayarak eğriler elde edebiliriz. Bu bağlamda aşağıdaki model hâlâ lineardir.
$$ y = \beta_0 + \beta_1x_1 + \beta_2x_2^2 + \beta_{12}x_1x_2 + \epsilon $$
Diğer bir deyişle, linear regresyon ile veriye uyan polinomu bulmak mümkündür. [1]
Kısaca polinomları hatırlarsak:
Poly: many Nomial: name, term
$Ax^n$ where $n\geq0$ and integer
Polinom en basit durumda, bir doğru, ikinci derece parabole karşılık gelecektir.
İyi de neden linear regression demişler madem yalnızca doğru üretmiyor?
Bunun için önce modeli sonra da çözüm yöntemini açıklamak gerekiyor.
Öncesinde, biraz terminoloji.
- Simple Linear Regression: bir bağımsız değişken ile
- Multiple Linear Regression: birden fazla bağımsız değişken ile,
bir bağımlı değişkenin tahmin edilmesidir. Anlatması kolay olan ile başlayalım.
Öncelikle kullanacağımız temel terimleri tanımlayalım. Biraz daha terminoloji:
| Gösterim | Ad | Açıklama |
|---|---|---|
| $\beta$ | parametre | |
| $x$ | bağımsız değişken | açıklayıcı değişken (explanatory variable) |
| $y$ | bağımlı değişken | response |
olmak üzere; basit linear regresyon doğrusu aşağıdaki gibi genellenir.
$$ y = \beta_0 + \beta_1x_1 + \epsilon $$
| Parametre | Açıklama |
|---|---|
| $ \beta_0 $ | kesme noktası |
| $ \beta_1 $ | eğim |
| $ \epsilon $ | rassal hata |
Örnek bir veri seti üzerinden $\beta_0$ ve $\beta_1$ için $\hat{\beta_0}$ ve $\hat{\beta_1}$ tahminleyicilerini bulmak istiyoruz. Ayrıca dikkat edelim, y değerini tam olarak hesaplamıyoruz, her zaman bir de rassal hata $\epsilon$ var. Doğal olarak bu hatanın en azlanmasını hedefliyoruz.
Basit Bir Örnek
Zamana göre yayılan bir talep, yıllara göre ev fiyatları, sınıftaki öğrencilerin boy-kilo ilişkisi, gibi klasik örnekler sıralanabilir. Tabii, zamansallığı ve otokorelasyonu yok sayıyoruz şimdilik. X ekseninde bağımsız değişken olur, Y eksenindeki değer ise x’e bağlı değişmektedir. Amacımız eldeki x’leri öğrenerek gelecekte karşılaşacağımız bir x değeri için y değerini tahmin etmektir. Peki, eldeki x’leri nasıl öğreneceğiz? Veriye uyan en iyi doğruyu (eğriyi, polinomu) bularak.
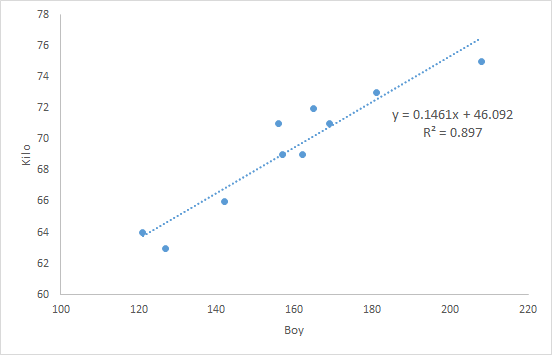
Boya göre kiloyu tahmin etmek istiyor olalım. Doğrusal ilişki, grafikte açık. Basit regresyon denklemini de excel veriyor.
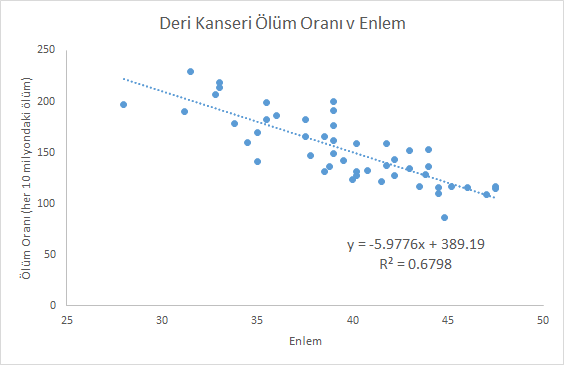
Bir diğer örnek, deri kanserinden ölüm riskini bölgenin coğrafi enlemine göre inceliyor. Yüksek enlemlerde yaşayan insanlar zararlı güneş ışınlarına daha az maruz kaldıkları için, deri kanserinden ölüm riski de düşüyor. İlişkide bir trend görülse de verilerin dağıldığı da açıktır. [3]
Model ve Mantığı
Öyle bir doğru istiyoruz ki, eldeki verilerin doğruya uzaklığı en az olsun. Doğruyu bulmanın en yaygın yollarından biri de “linear least squares fit”. Amaç fonksiyonu şöyledir:
$$ \min \sum_{i=0}^{len(obeserved)-1} (observed[i] - predicted[i])^2 $$
Burada (observed - predicted) farkının diğer bir deyişle uzaklığın nasıl hesaplandığı üzerinde durmalıyız.
Hangi uzaklığı kullanacağız? X, Y, P?
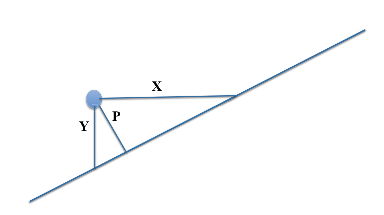
Y uzaklığını kullanacağız çünkü verilen x bağımsız değişkeni için y değerini tahmin etmek istiyoruz. Ayrıca düşey uzaklık (Y), tahmindeki hatayı da ölçecektir. Bazı durumlarda dik uzaklık (P) tercih edilmektedir. Yatay uzaklık (X) ise tek başına anlamsız olacaktır.
Ayrıca düşey uzaklığa, “residual” diyoruz. residual = actual - predicted
Residuallar, ölçüm hatası gibi rassal faktörlerden ya da bilinmeyen rassal olmayan sebeplerden kaynaklanabilir. Misal, boya bağlı olarak kiloyu tahmin etmeye çalışıyorsak, bilinmeyen faktörler diyet, egzersiz, vücut tipi ya da farklı genetik sebepler olabilir.
Neden karesini alıyoruz?
- Karesini alarak, residualın pozitif veya negatif olması durumunu ortadan kaldırıyoruz.
- Karesini almak, büyük residuallara daha fazla ağırlık(önem) veriyor ama büyük olanın her zaman domine edeceği kadar değil.
- Eğer residuallar korelasyonsuz (uncorrelated) ve ortalaması 0, sabit (ama bilinmeyen) varyans ile normal dağılıma sahip ise least squares fit aynı zamanda kesme noktası ve eğim parametrelerinin maximum likelihood tahminleyicisidir. [6]
Gelelim asıl anlatmak istediğim konuya. En iyi uyan doğruyu(best fitting line) diğer bir deyişle residualların en kısa olduğu, hatanın en az olduğu doğruyu nasıl buluyoruz?
2 boyutlu bir uzayda, eksenler a ve b olmak üzere herbir (a, b) noktası bir doğruyu (y = ax + b) temsil edecektir.
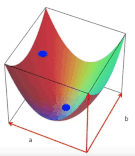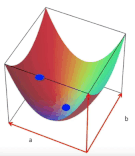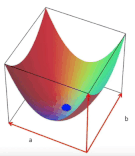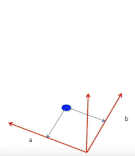
Bu 2 boyutlu uzayın üzerinde bir yüzey hayal edelim, yüzeyin yüksekliği amaç fonksiyonumuza eşit olacaktır ve kareler toplamından dolayı yüzeyin şekli her zaman konveks olacaktır. Yüzeyin en alt noktası, amaç fonksiyonunu optimal yapan çözüme karşılık gelecektir. Diğer bir deyişle, aradığımız en iyi doğruyu verecektir.
Yine iyi bir görselleştirme olduğunu düşündüğüm diğer örnek de [5]‘den alınmıştır. Adım adım açıklamak gerekirse:
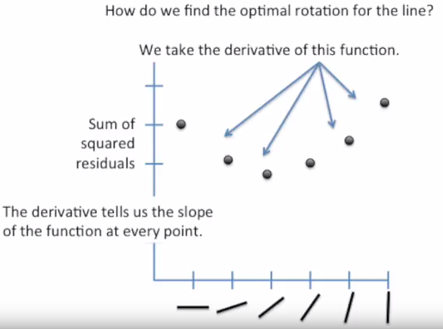
- Başlangıçta bir doğru çizeriz ya da üstteki açıklamaya göre eksenleri a ve b olan iki boyutlu uzayda bir (a, b) noktası seçeriz. Bu başlangıç çözümümüzdür.
- Her adımda yeni (a, b) ikilisi seçerek amaç fonksiyonunu yenileriz. Komşu çözüm üretiriz.
- Amaç fonksiyonunun (hatanın, least sum of squares) en az olduğu (a, b) ikilisinde dururuz.
- Konveks şekil sayesinde optimal çözüme her zaman ulaşırız. Lineer regresyon, aslında konveks optimizasyon problemlerine bir örnektir.
Başlangıçta sormuştuk, “İyi de neden linear regression demişler madem yalnızca doğru üretmiyor?” diye. Çünkü gradient descent (eğimli iniş) algoritmasıyla yukarıdan aşağıya doğrusal olarak iniyor.
Multiple Linear Regression
Tek bağımsız değişkene bağlı analiz (simple linear regression) gerçekte nadiren karşımıza çıksa da anlatması ve görselleştirmesi kolay olduğu için genelde onun üzerinden anlatılır. Multiple regresyon’a örnek olarak [3]‘deki veri setini kullandım. Veri seti, 94-98 yılları arasında Ankara’nın hava durumuna ait bilgiler içeriyor. 10 feature (kolon) ve toplam 321 satır var.
| Feature | Domain |
|---|---|
| Max_temperature | [23.0, 100.0] |
| Min_temperature | [-7.1, 65.5] |
| Dewpoint | [-3.1, 57.6] |
| Precipitation | [0.0, 4.0] |
| Sea_level_pressure | [29.46, 30.6] |
| Standard_pressure | [26.3, 27.18] |
| Visibility | [0.2, 11.5] |
| Wind_speed | [0.0, 18.0] |
| Max_wind_speed | [2.19, 57.4] |
| Mean_temperature | [7.9, 81.8] |
Sonuçta elde edilen linear-regresyon modeli:
Mean_temperature =
0.55 * Max_temperature +
0.3323 * Min_temperature +
0.0597 * Dewpoint +
-9.2456 * Sea_level_pressure +
7.5 * Standard_pressure +
0.1113 * Visibility +
0.0728 * Wind_speed +
76.445
ve çözüm özeti:
Correlation coefficient 0.994
Mean absolute error 1.2509
Root mean squared error 1.6323
Relative absolute error 9.7276 %
Root relative squared error 10.8671 %
Total Number of Instances 321
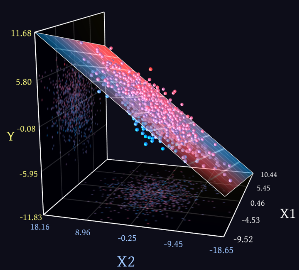
Bu yazının esas amacına dönelim tekrar. Çözüm mantığı aynı mı? Evet, aynı. Her ne kadar 10 boyutlu veri setini anlamlı şekilde görselleştiremesek de 10 boyutlu uzayda, 9 boyutlu cismi veriye uydurmaya çalışıyoruz. Tıpkı yukarıda 2 boyutlu uzayda, 1 boyutlu doğruyu aradığımız gibi. 3 boyutlu veri olduğunda ise, en iyi 2 boyutlu düzlemi ararız.
Grafik Miabella AI adlı siteden alınmıştır. Sitede bir de interaktif demo var, 3D canlandırma açısından faydalı olabilir.
Sonuç Ne Kadar İyi ?
Dikkat ettiyseniz, amaç fonksiyonumuz modelin (çözümün) iyiliği hakkında bilgi vermiyor ve değeri bizim kullandığımız verilere göre değişiyor. Elimizdeki probleme göre çok büyük bir amaç fonksiyonu değeri ile “iyi” bir model kurmuş da olabiliriz, ama olmayabiliriz de. Diğer bir deyişle, verinin değerinden bağımsız (scale independent) bir ölçüye ihtiyacımız var. $R^2$, determinasyon katsayısı, scale independent ölçülerimizden biri.
$$R^2 = 1 - \frac{\sum_i(y_i - p_i)^2}{\sum_i(y_i-\mu)^2}$$
Bölünen, (nam-ı diğer SSE, Sum of Squared Errors) tahmindeki hataya; bölen (nam-ı diğer TSS, Total Sum of Squares) ise gerçek verideki değişkenliğe karşılık gelmektedir. Aslında aşağıdaki gibi ifade edersek daha açık olacaktır:
Varyans formülünde, “n = sample size” bölenleri birbirini götüreceği için formül yukarıdaki gibi sadelişiyor.
$$R^2 = \frac{var(mean) - var(fit)}{var(mean)}$$
Bağımsız değişkenler, bağımlı değişkenin varyansının $R^2$ kadarını açıklıyor, şeklinde yorum yapılabilir. “$R^2 = $ Explained Variation / Total Variation”
$$0 \le R^2 \le 1$$
Genel anlamda $R^2$, 1’e ne kadar yakınsa o kadar iyidir, ama her zaman değil. (bknz: residual plots)
Bitirirken
Uzun zamandır yazmak istediğim bir konuydu. İstediğim tüm başlıkları da anlatamama rağmen oldukça uzun bir yazı oldu. Umarım açıklayıcı olmuştur. Sorunuz, eleştiriniz, öneriniz varsa lütfen çekinmeden yazın.
Sonraki konularda ele alacağım başlıklar, kendime not:
- Assumptions of linear regression
- Residual analysis, goodness of fit
- Polyfit and cross validation
- Solving linear regression with simplex
- A better example for Multiple Linear Regression
Kaynaklar
- [1] Regression Analysis, Shalabh, IIT Kanpur
- [2] Skin Cancer Example
- [3] Weather Ankara Data Set
- [6] Think Stats, v2, p.138. Allen B. Downey.
