Tanımlayıcı istatistiklerden ortalama ve ortanca. Analiz yapılırken iş bu ikisinden hangisinin anlamlı olduğuna geldiğinde sık sık hata yapılmaktadır. Hataların yanısıra, dünyada bu istatistiklerin manipüle edilerek kötüye kullanıldığı örnekler de ne yazık ki çoktur. (bknz: statistical lies) Ne zaman hangisi kullanılmalıdır, basitçe açıklayalım.
Ortalama, herkesin iyi bildiği terimlerden biri, tüm değerleri topla / kaç değer varsa ona böl.
Ortanca (medyan), adı üstünde, veriler sıralandıktan sonra tam ortadaki değerdir. Diğer bir deyişle, verilerin yarısına büyük-eşit yarısına da küçük-eşit olan değerdir.
“Ne zaman medyan kullanılmalıdır?”, sorusuna verilecek belki de en klasik örnek, vatandaşın gelirini gösteren veri setidir.
1 1 1 1 1 1 1 1 1 1
2 3 4 4 4 4 4 5 5 5
Yukarıdaki veri seti için, ortalama = 2.5, ortanca = 1.5 gelecektir. Hatta farkı daha iyi görmek adına, son değeri 5*10^6 yaparsak, ortalama 250*10^3'ün üzerinde olacaktır. Varsayalım ki bu veriler, X Distopyasındaki insanların gelir dağılımı olsun. Bir kişinin geliri 5 milyon iken memleketin yarısı 1, onlardan hallice bir grup da 2 3 4 gelire sahipler.
Eğer çıkıp dersek ki; bu memleketin gelir ortalaması 250,000’dir. Çok anlamlı olmaz. Doğal olarak burada kullanılması gereken istatistik medyandır. Çünkü veri simetrik dağılmamıştır.
Dağılım simetrikleştikçe, ortalama, medyan ve mod birbirine yaklaşacaktır. Tam simetriklik durumunda eşit olacaklardır. Normal dağılmış bir veri seti için, bu durumu aşağıdaki grafikte görmekteyiz.
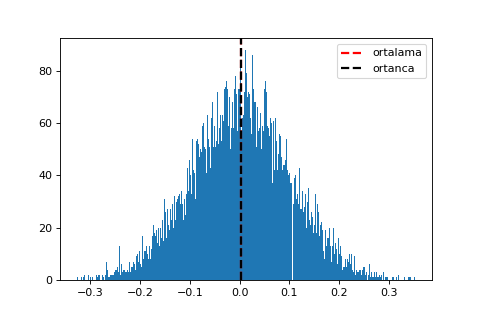
Veri simetrik dağılmamışken, ortalama (mean) aşırı uçlardan (outlier) etkilenirken, medyan bize daha anlamlı bilgiler sunacaktır. Çarpık dağılımlarda, ortalama, çarpıklığın olduğu tarafa doğru kayacaktır. Örneğin, aşağıda sola çarpık dağılımda ortalama, ortancanın solunda kalmıştır.
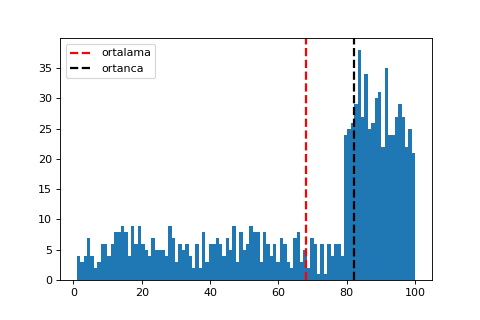
“Hangisini kullanmalıyız?"‘ın cevabı, “neyi aradığımızda” gizlidir. Örneğin;
Önceki örnekteki gibi gelir dağılımıyla ilgileniyorsak
medyan değerini kulllanmalıyız. Çünkü medyan bize, populasyondan seçilecek ortalama (tipik, standart, orta direk) bir vatandaşın geliri hakkında en iyi tahmini verecektir ve populasyonu daha iyi temsil edecektir. Özetlemek gerekirse;
- Ortalama (Mean): Ortalama gelir nedir?
- Ortanca (Medyan): Ortalama bir vatandaşın geliri nedir?
Türkiye’deki şehirlerin ortalama nüfusu
“Eğer ki herkesi göç ettirip nüfusu memlekete eşit dağıttığımızda ne olur?” sorusunu araştırmıyorsak, medyan kullanılmalıdır. Aksi halde, İstanbul gibi nüfusu yüksek şehirler, yukarıdaki örnekte 5 milyon gelire sahip kişi gibi davranabilir.
Bir anket yaptık, müşteri memnuniyetini ölçmek adına
Yine medyana dikkat edilmelidir. Yukarıdaki örnek veri setini tekrar ele alalım. 5 - çok iyi, 1 - çok kötü, 3 - orta seviye puan olsun. Sadece ortalamaya bakıldığında, 2.5 puan ile, sistem “idare eder, orta seviye” puana sahiptir yorumu bizi yanlış yönlendirecektir. Müşterilerin yarısının 1 puan verdiği gözden kaçabilir. Medyan = 1.5, orta seviyenin altında daha gerçekçi bir değerlendirme olur.
Medyanın, aritmetik ortalamaya tercih edilebileceği bir durum da verilerin sayısal olmayıp sıra dizisi olduğu durumdur.
Örneğin; bir ankete verilebilecek cevaplar, “çok iyi”, “iyi”, “nötr”, “kötü” ve “çok kötü” olsun. Medyan olduğu gibi çalışacakken, aritmetik ortalamayı kullanabilmek için bu cevap seçeneklerine bir çeşit katsayı atanmalıdır.
Bazı durumlarda ise her iki metrik de anlamlıdır.
Ortalama enerji tüketimi
- Eğer “ortalama bir vatandaşın tükettiği enerji” araştırılıyorsa medyana dikkat edilmelidir.
- Eğer “enerji tüketimi eşit dağıtılırsa bir kişi ne kadar enerji harcamış olur” araştırılıyorsa ortalamaya bakılmalıdır.
Müşterilerin sistemde harcadıkları para
- Müşteri sayısıyla çarpıp toplam geliri kolayca hesaplamak için “ortalama”
- Ortalama bir müşterinin harcadığı para araştırılıyorsa yine medyan anlamlı olacaktır.
Özetlemek gerekirse, medyan aşırı uçlardan daha az etkilendiği için, genelde, populasyonu daha iyi temsil eder. Ancak; her zaman önce veri seti görselleştirilmelidir ve verilerin nasıl dağıldığı incelenmeli, varyans dikkate alınmalıdır. Hızlıca analize geçip rakamları toplayıp bölmeden önce, neye cevap arandığı iyi belirlenmelidir.
Ayrıca (bknz: trimmed mean, winsorized mean)
